20 UCAT Quantitative Reasoning Tips: Save Time and Boost Your Score
Quantitative Reasoning (QR) is a section that divides students. There are the adept mathematicians who breeze past it, and then there’s the not-so-number-savvy students.
The good news is that there's always room for improvement. A lot of this test is about having a solid understanding of the fundamentals. You can learn how to lay these foundations to improve your score.
If you've already started preparing, try some free UCAT practice questions to get an overview of all UCAT sections

How to prepare for Quantitative Reasoning
The fact: Most students find the majority of QR questions easy (you're tested on basic concepts like percentages and rates, not integration or complex numbers).
The mystery: If most students find the questions easy then why don’t most students score highly in this section?
The answer: Timing! When you only have 41 seconds per question, you don’t have time to think deeply about how to approach the problem – you just have to ‘get it’ as you read the question. Our tips should help you just ‘get it’ more often.
Check out our UCAT FAQ article for UCAT costs, dates, and much more
Table of contents
1. Know all the key question types inside out
2. Think about timing and pace
3. Refine your mental calculation skills
4. Don’t hesitate to use the calculator when you need to
5. Use the memory function on the calculator
6. Practise using a computer with a number pad
7. Master the keyboard shortcuts
10. Flag and move on if you're stuck
12. Get into the habit of interpreting charts and graphs
13. Know your units and how to convert them
14. Familiarise yourself with common fractions and percentages
15. Be comfortable converting between hours and minutes
16. Understand compound interest
20. Sit mock exams under timed conditions to find your weaknesses
1. Know all the key question types inside out
The UCAT QR section asks GCSE-level maths questions around the key areas of percentage, unit conversions, rates and averages.
Focus your UCAT revision around these mathematical concepts, giving particular attention to the areas that you don’t feel that confident in.

2. Think about timing and pace
Answering 36 questions in 25 minutes gives you 41 seconds per question.
Remember that this is an average. Some questions can be solved in under 30 seconds, whereas others may take a minute or longer due to their difficulty or requirement for multiple steps.
Learn more about UCAT timing (this is one area you really need to get comfortable with).
3. Refine your mental calculation skills
Develop mental calculation skills to save precious time that can be used to tackle harder questions.
4. Don’t hesitate to use the calculator when you need to
The UCAT has an inbuilt calculator (Medify’s calculator is identical).
When you face a question outside the scope of your mental maths skills, pull out your onscreen calculator.
Check out 8.5 tips to master your primary QR tool (the calculator!).

5. Use the memory function on the calculator
Have you ever wondered what those ‘M’ buttons are on the calculator? These are memory functions:
- Press M+ to add a number to the memory
- Press M- to remove the stored number
- Press MRC to recall the stored number
This is often useful for multi-step questions.
![UCAT calculator, highlighting the [MRC], [M+], [M-] memory buttons](https://assets-global.website-files.com/5d3ac7a15216e3b85a929e54/647f1d75aff3e31334abfbcd_QR_TIPS_8.png)
6. Practise using a computer with a number pad
The number pad is ergonomically designed to increase efficiency when typing compared to the horizontal number keys.
Use a keyboard with a number pad for your UCAT practice, as you will have access to one in a real exam.

7. Master the keyboard shortcuts
- Use Alt+C to open and close the calculator
- Use the Backspace button for ON/C (clearing the calculator)
- Use the keyboard (+,-,*,/) for addition, subtraction, multiplication and division
8. Use the notebook and pen
For questions involving a number of mathematical operations, the notebook and pen provided at the test centre can be useful for jotting down key intermediate working steps.
9. Don’t be afraid to guess
There is no negative marking in the UCAT. For difficult questions, narrow down your choices and guess the answer before moving on.
10. Flag and move on if you're stuck
It's easy to become obsessed with getting a question right and dwell on it for minutes, when you could’ve answered three other questions!
If you face a question that you have no clue how to solve, have a quick guess, flag it, and move on. Flagging allows you to revisit a question at the end of a section, if there is time left over.
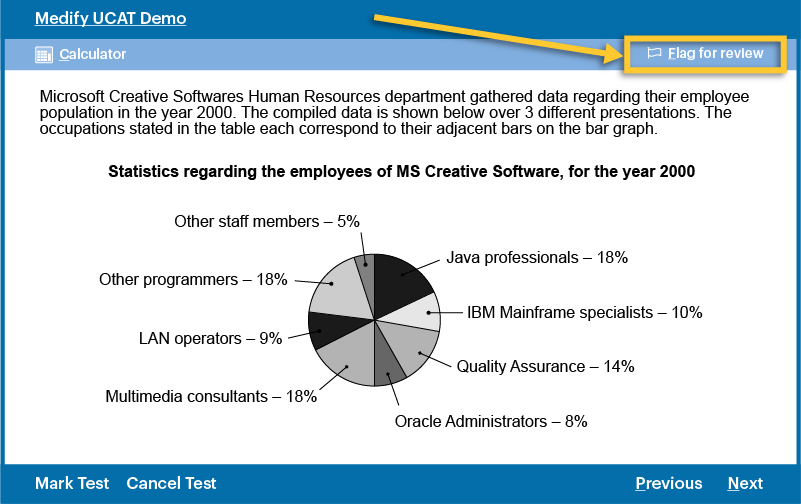
11. Repetition is key
When you solve practice questions regularly, you soon realise that many questions have a pattern. It’s then just a matter of recognising which numbers to pull together.
At first, start working on your practice questions without worrying about the time limit. Gradually increase your speed and build momentum towards your UCAT exam.
Our UCAT Skills Trainers work with repetition to build core UCAT skills into your muscle memory and are included with all UCAT packages
12. Get into the habit of interpreting charts and graphs
Some UCAT QR questions require you to interpret data from graphs (e.g. histograms, pie charts, line charts) and tables.
Get into the habit of interpreting data presented in TV news, magazines, newspapers and other media outlets to weave UCAT preparation into your daily life.
13. Know your units and how to convert them
Always be mindful of your units:

14. Familiarise yourself with common fractions and percentages
Know how to convert common fractions to percentages and vice versa to save time:
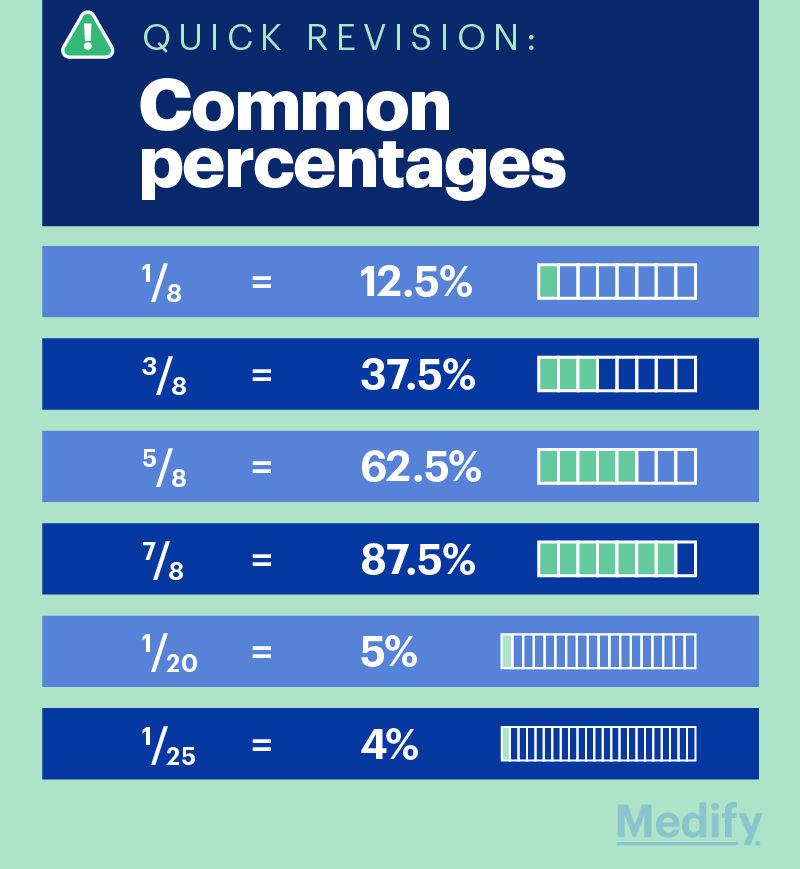
15. Be comfortable converting between hours and minutes
Become familiar with the common minute-hour equivalents:

16. Understand compound interest
Interest compounds over time and a 5% return in one year does not mean a 10% return in two years. The return in the second year will be the original amount x 1.05 x 1.05.
There are often distracting answer options that don’t include the compound interest.
17. Understand tax brackets
Questions involving tax brackets are often featured in the QR section. The key to understanding the tax bracket is knowing that you don’t calculate the tax at a flat rate.
Instead, the first specified portion of the income is taxed at a low rate (or no tax), and the next specified portions gradually get taxed at higher rates.
For example, in England and Wales, the following rates apply to taxable incomes:

Based on the above tax bracket, the tax payable for a doctor earning £170,000 would be:
- Tax on first £12,500 = £0
- Tax on next £37,500 = £37,500 x 0.2 = £7,500
- Tax on next £100,000 = £100,000 x 0.4 = £40,000
- Tax on next £20,000 = £20,000 x 0.45 = £9,000
Total tax payable = £0 + £7,500 + £40,000 + £9,000 = £56,500
18. Areas and volumes
Learn the formulas for the areas and volumes of common shapes:

19. Get into the zone
Most people are prone to making mistakes under stress. For example, you might forget to enter a decimal point in the calculator.
You need to stay calm throughout the question solving process. First, remember that the questions are no harder than GCSE mathematics and you have all the skills to tackle the questions.
Second, practise under timed conditions to emulate the pressure of exam conditions so that you can get used to it.
The graph below shows that some stress is good. Performance actually increases with stress until an optimal point. After that, performance drops off rapidly. The key is to channel your stress into targeted exam practice, and realise when you need to take a step back.

20. Sit mock exams under timed conditions to find your weaknesses
Practise answering UCAT QR questions under timed, pressured conditions to accurately diagnose your weaknesses.
Medify’s mock exams use an enormous data set to compare your performance against the average time users take to reach the correct answer. We're constantly updating and improving our mock exams to offer you the most test-like experience.
Summary
- Fully understand the type of questions asked in the UCAT QR section.
- Be mindful of the time limit and don’t dwell on one question. Make educated guesses, flag and come back if required.
- Get up to speed with your mental maths calculations and use of the provided tools (notebook, pen, calculator).
Access example video responses to interview questions from real students
Succeed in your medical school interview. Start today for only £25
Membership will expire on 31 March 2024 23:59 UK time
Boost your BMAT score with 2,000+ practice questions
Write your personal statement. Try Medify Today
2 in 3 students prepared for UCAT with Medify. Try Medify Now
Boost your UCAT score with 24 mocks and 40+ mini-mocks
2 in 3 students prepared for UCAT with Medify. Try Medify Now
Boost your UCAT score with 24 mocks and 40+ mini-mocks
Boost your BMAT score with 2,000+ practice questions
Write your personal statement. Try Medify Today
2 in 3 students prepared for UCAT with Medify. Try Medify Now
Boost your UCAT score with 24 mocks and 40+ mini-mocks
2 in 3 students prepared for UCAT with Medify. Try Medify Now
Boost your UCAT score with 24 mocks and 40+ mini-mocks
2 in 3 students prepared for UCAT with Medify. Try Medify Now
Boost your UCAT score with 24 mocks and 40+ mini-mocks
